Wang Tiles and Turing Machines

Posted on October 12, 2012 by Graham Shawcross

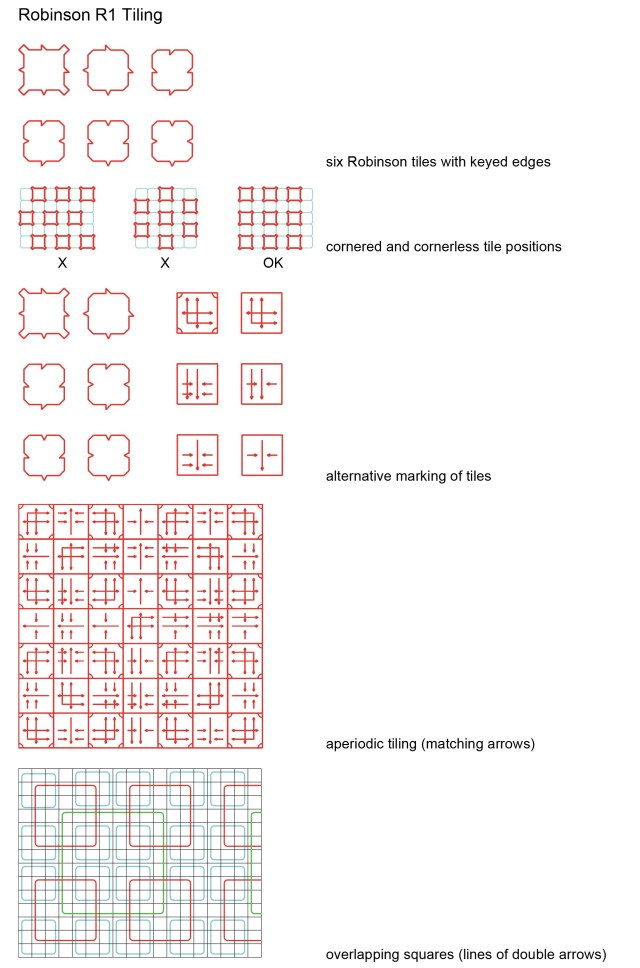
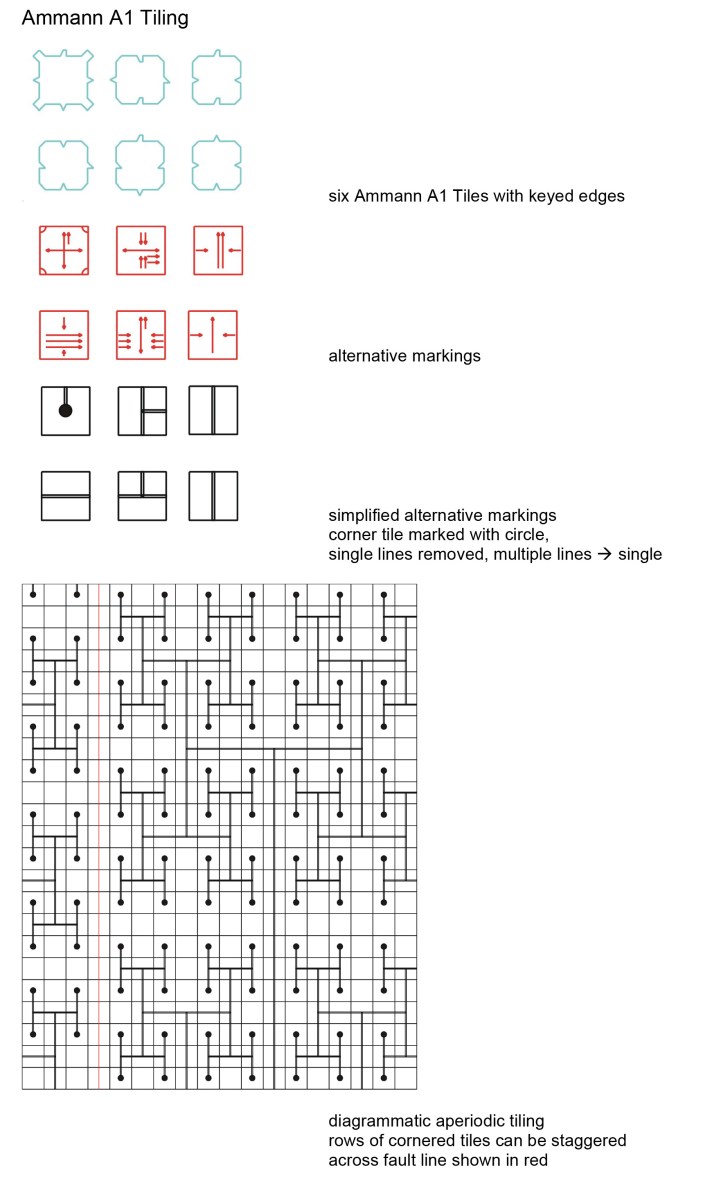
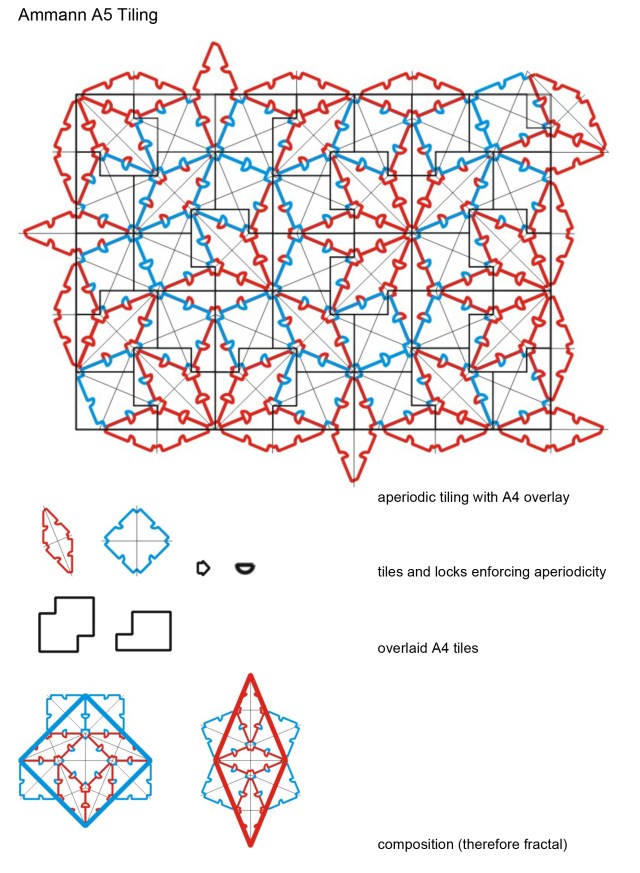
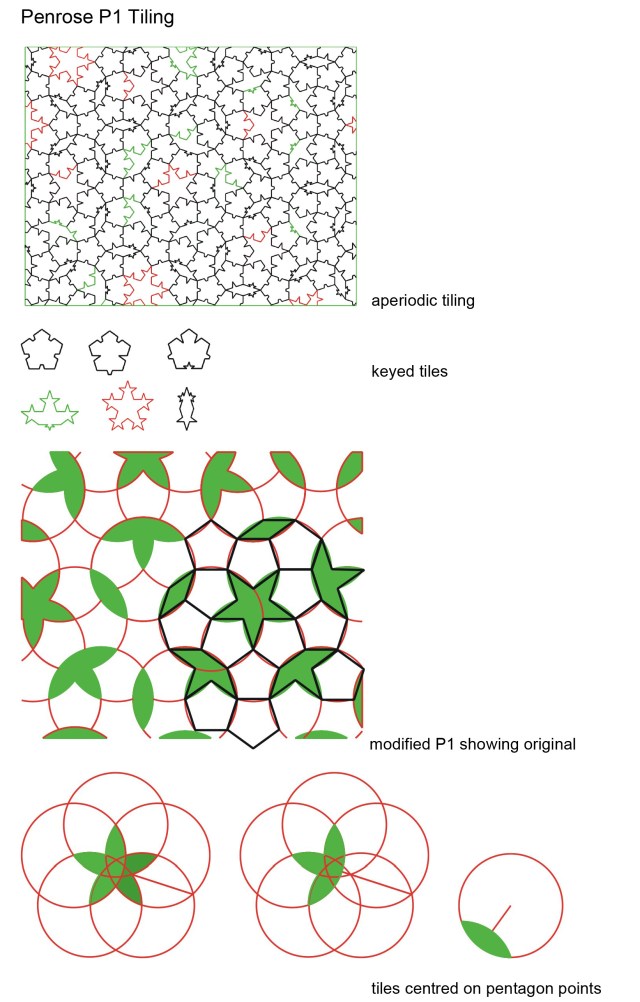
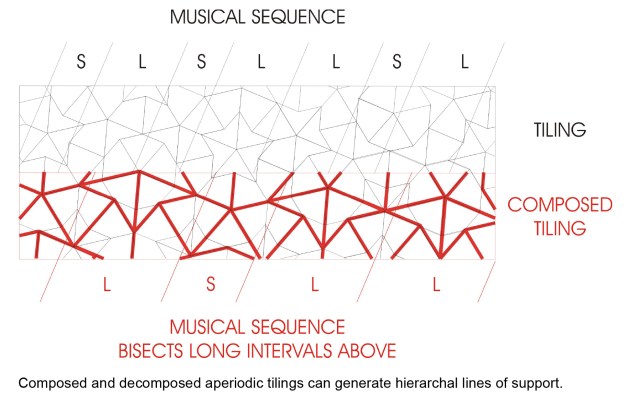
Wang pointed out that it is possible to find sets of Wang tiles that mimic the behaviour of any Turing Machine (Wang 1975).

A Turing machine can compute all recursive functions, that is functions whose values can be calculated in a finite number of steps. That is to do, however inefficiently, what any conceivable computer can do.

The basic idea is to use rows of tiles to simulate the tape in the machine, with successive rows corresponding to consecutive states of the machine.

The following examples are based on those in “Tiling and Patterns” (Grünbaum and Shephard 1987) with coloured tiles replacing numbered tiles, and initialisation somewhat simplified.

Simple Addition Using Wang Tiles

This example uses one quarter of the plane, bounded by grey tiles, it shows the addition of two positive integers, a and b, and for convenience it is assumed that 2 ≤ a < b.

In this slightly simplified presentation step 1 consists of placing tiles to indicate the numbers to be added together (5 and 9 in this case) and a start signal in the top left-most square.

Step 2 then consists of adding the only possible tiles next to those that have already been placed and step 3 shows the signal beginning to take a diagonal path downwards. This continues, using tiles from column B, until it meets the tiles descending from the first number, with tiles from column C. At the meeting point a series of horizontal tiles, from column D, is generated  which changes direction when it meets the tiles descending from the second number. The signal then moves diagonally upwards, using tiles from column F, until the process terminates at the top edge where its position indicates the required answer.

 

The colour numbers above are those used by Grünbaum and Shephard and the tiles are the same except that a missing one has been added and the tiles have been arranged in a slightly different manner. Incidentally using coloured tiles rather than numbered ones meant that the missing tile was much easier to spot.

Generating the Fibonacci Sequence

The following example is presented without a complex narrative. It shows all the steps on one diagram, follows a similar method to the previous example and is otherwise I think self explanatory.

 
/Users/grahamshawcross/Documents/blog_drafts/Wang Tiles and Turi

Diagram above corrected 08/05/2015

Generating Prime Numbers

The final example illustrates the ingenuity that can be required to carry out some computations, it is due to E. F. Moore and M. Fieldhouse and was communicated to Grünbaum and Shephard by H. Wang. Here the only change I have made is to use colours rather than colour numbers.

The tiling uses 30 prototiles and forces a tiling that places tiles marked P or C at the prime and composite positions in the top row. The tiles are marked with letters as well as being coloured and it can be seen that they build up blocks of squares which increase in size downwards. These square blocks are indicated by thickened lines.

The tiles marked by an asterisk are used to generate the blocks down the left boundary and the tiles with superscript C transmit a signal to the effect that the number is composite. These composite signals are generated by the tiles by B* (which is only used once) and D4 (which occurs on the top right corner of each square block that does not abut on the left boundary of the tiling). They are absorbed by the tiles C on the top line, and D6 on the bottom right corner of certain blocks. When the signal is absorbed in this way it is regenerated higher up by a D4.

The increasing blocks signal to the top row when a number has a proper divisor greater than 2. Divisibility by 2 is taken care of by alternating A and B tiles in the second row. Either can transmit the composite signal. The special tile B* is introduced simply to ensure that a prime tile P appears in position 2. This does however seem to introduce a degree of circularity.

The use of colours again revealed an error in the designation of one edge of the bottom right tile in the tile set.

Bibliography

Grünbaum B., Shephard G. C. (1987)
Tilings and Patterns
W.H. Freeman and Company
New York
 
Wang H. (1975)
Notes on a class of tiling problems
Fundamental Mathematics 82(1975) Pages 295-305
 
Robinson R. (1971)
Undecidability and nonperiodicity for tilings of the plane
Inventiones mathematicae Vol 12, Pages 177-209
Posted in Aperiodic Tiling, Architecture, Geometry, Tiling, Turing | Tagged , , , , | 22 Comments

Wang Tiles and Aperiodic Tiling

Posted on October 12, 2012 by Graham Shawcross

Wang originally conjectured that no aperiodic tilings could exist. Wang was interested in the decidability of the Tiling Problem; it is said to be decidable if there exists an algorithm which will yield a solution for any given set of prototiles in  a finite number of steps or trials. The following is a simplified version of his approach (Grünbaum and Shephard 1987, page 602).

If a set of prototiles admits a tiling then one of these possibilities must hold:

(a) the set admits only periodic tilings, for example just one regular hexagon.

(b) the set admits periodic and non-periodic tilings, for example a square.

(c) the set admits only non-periodic tilings, in other words is an aperiodic set.

Wang showed that the Tiling Problem is decidable if one only considers sets which satisfy (a) and (b). In 1961 he went on to conjecture that possibility (c) could not occur, at the time an entirely plausible assertion.

The discovery of an aperiodic set spoilt Wang’s argument and it is now known that the Tiling Problem is undecidable.

The first aperiodic set was found by Wang’s student Berger (1966) and consisted of 20,426 tiles. This was first reduced by Berger to 104 tiles, then by Knuth to 96.

Other aperiodic tilings have since been used to produce smaller sets of aperiodic Wang tiles, from 32 to 24 and 16 as shown below.

According to Grünbaum and Shephard (Grünbaum and Shephard 1987, page 596).

“The reduction in the number of Wang tiles in an aperiodic set from over 20,000 to 16 has been a notable achievement. Perhaps the minimum possible number has now been reached. If, however, further reductions are possible then it seems certain that new ideas and methods will be required.”

Kari suggested such a method and produced a set of 14 tiles over 6 colours (Kari 1996). This was reduced by Culik to 13 tiles over 5 colours (Culik 1998) and this appears to be the smallest known set, although together they have attempted to show that one tile can be removed from the set.

However for Architectural and Computer Graphics applications the smallest set is not necessarily the most desirable.

Penrose P2 to Wang Tiling (32 Tiles)

A set of 32 Wang tiles can be generated from an aperiodic Penrose P2 tiling. The following procedure was suggested by Penrose and refined by Robinson. It starts with a Penrose P2 tiling such as that below, although Grünbaum and Shephard suggest the procedure could be simplified by using a Penrose P3 Rhomb tiling.

1. Grid the Penrose Tiling

Cut up the Penrose P2 tiling by keeping as close to the horizontal and vertical as possible. In fact each patch is made up of Robinson’s A-tiles (kites, darts, half-kites and half-darts).

2. Catalogue the Cut-Up Shapes

Catalogue the cut-up shapes using the dot and arrow matching rule for Penrose P2 Tiling (each type of dot must match and arrows be in same direction).

3. Assign Colours to Edges of Cut-Up Shapes

Using the following colours

Assign colours to vertical and horizontal edges respecting and the encoding by dots and arrows as follows:-

4. Assign A Wang Tile to Each Cut-Up Shape

Assign Wang tiles to each of the cut-up shapes including their rotations and reflections using the encoded edge colours. The rotations and reflections are required because Wang tiles do not permit rotation or reflection.

5. Assign Appropriate Wang Tiles

Replace the gridded P2 Tiling with the corresponding Wang tiles:-

This is the Wang tile equivalent of the original Penrose P2 tiling shown at the the start of this section, using 32 tiles over 16 colours.

Ammann A2 to Wang Tiling (24 Tiles)

Ammann A2 tiles can have unit length sides, so the prototiles can be made up of collections of 3 squares and 5 squares.

Because Wang tiles cannot be rotated or mirrored each of the possible orientations of the A2 prototypes needs to have its own unique set of Wang tiles.

1. Create a Set of 24 Wang Tiles Using 24 Colours

The 24 colours on the left are used to generate the 24 unique Wang tiles on the right.

2. Map the 24 Wang Tiles onto 8 Prototiles

The Wang tiles are then mapped onto the 4 possible orientations of  Ammann A2 prototiles (8 tiles in all as listed in the diagram below).

As indicated by the orientation of the coloured triangles in the colour list above, the first row of colours is used on the top and bottom edges of the Wang and A2 prototiles; these both have to match other tiles edge to edge. Similarly the second row of colours is used on the left and right hand edges of both sets of tiles.

The third and fourth rows are used for the top and bottom edges of the Wang tiles that become the internal edges of the A2 prototiles.

Rows five and six  are used for the left and right hand internal edges of the A2 prototiles.

The functional arrangement of the colours above differs from Grünbaum and Shephard, but the numbers above and below them are those that they used.

3. Allow Duplication Between 3 and 5 Square Prototiles

The red numbered Wang tiles in the prototile catalogue represent the tiles that are used in both the 5 and 3 square A2 prototiles and allowing these duplications allows the number of Wang tiles to be reduced to 24.

Ammann A2 to Wang Tiling (16 Tiles)

A sets of 16 Wang tiles can be generated from the Golden Section version of the same aperiodic Ammann A2 tiling marked with 2 sets of parallel Ammann bars. These form overlapping red and cyan grids.

1. Catalogue the Tiles formed by the Cyan Grid

Using the cyan grid to provide the edges of a new set of tiles and the red grid to create the markings that provide the matching conditions, catalogue the different tile types (outlined in blue and numbered below).

According to Grünbaum and Shephard this results in the following 16 tiles (although tile 6 does not appear to be present above)

2. Map the Catalogued Tiles to Wang Tiles

Map the 16 catalogued tiles above to the 16 Wang tiles below using 6 colours.

A further set of tiles can be generated that correspond to composed or decomposed versions of the tiles above.

3. Apply the Wang Tiles to the Original Tiling

A Wang tiling can then be generated that corresponds to the original Golden Section Ammann A2 tiling  using 16 tiles over 6 colours and with the composed tiling indicated by thickened lines.

/Users/grahamshawcross/Documents/blog_drafts/Wang Tiles and Aper

Smaller Sets

More recently smaller sets of Wang tiles have been found using an entirely different method due to Kari, (Kari 1996). This uses Mealy machines that multiply Beatty sequences of real numbers by rational constants. Using this method Kari produced a tile set of 14 tiles over 6 colours. Using a slightly modified version of Kari’s method Culik, Culik 1996, produced a set of 13 tiles over 5 colours.

The authors propose the following 13 over 5 colour Wang tile set.

Bibliography

Grünbaum B., Shephard G. C. (1987)
Tilings and Patterns
W.H. Freeman and Company
New York
 
Kari J., 1996
A small aperiodic set of Wang Tiles
Discrete Mathematics 1996 Volume 160 Issue 1-3 Pages 259-264
 
Culik K., 1996
An Aperiodic Set of 13 Wang Tiles
Discrete Mathematics Volume 160 Issue 1-3 Pages 245-251
Posted in Aperiodic Tiling, Architecture, Geometry, Tiling | Tagged , , | 13 Comments

Aperiodic Tiling

Posted on October 12, 2012 by Graham Shawcross

This closely follows “Tilings and Patterns” (Grünbaum and Shephard, 1987), but uses coloured diagrams rather than their monochrome ones. In some ways this is simply a catalogue of aperiodic tilings, their various forms and some indication of their uses, but my interest comes from their ability to be at the same time both regular in form, and random in distribution.

Aperiodic tiling can only tile the plane in a non-repeating manner. This is in contrast to non-periodic tiling that can tile the plane in an irregular manner but can also do so in a regular, periodic fashion.

Aperiodic tilings often requires that tile edges be marked, coloured or keyed in some way to force aperiodicity, and a number of examples are illustrated below.

Aperiodic Tilings are usually named for their originators, there are Wang, Robinson, Ammann and Penrose tilings. Where an originator has more than one tiling to their name these are designated as follows Ammann A2 tiling, Penrose P3 tiling etc.

Wang Tiling

Wang tiles consist of square tiles with coloured edges, which must be placed edge-to-edge. They tile the plane following the rule that adjacent tiles must have matching edge colours. Rotation or reflection of tiles is not allowed.

The tiles above can also be coloured as follows:-

With physical tiles the prohibition on rotation can be enforced by a trivial shape modification:-

admin-ajax

The matching conditions (colours) can also be represented by numbers, as is done in “Tilings and Patterns”  (Grünbaum and Shephard, 1987).

Wang tiles can be used to mimic any Turing Machine where rows of tiles simulate consecutive states of the machine, this is the subject of a separate post, “Wang Tiles and Turing Machines”.

Methods have been developed that use the other aperiodic tilings to generate very small sets of Wang tiles and these are described in another post, “Wang Tiles and Aperiodic Tiling”.

Wang tile sets are usually described by the number of tiles in the set together with the number of different edge colours used, for example 13 tiles over 5 colours. This is currently the smallest known set.

Other Aperiodic Tilings

Robinson R1 and Ammann A1 tilings are both similar, using square tiles with keyed edges.

 

 

Ammann Bars

Robert Ammann proposed the use of linear markings (Ammann bars) to enforce aperiodicity on tile sets. This is achieved by requiring that the bars on adjacent tiles line through. These have been indicated on many of the tilings above, (the Ammann A1-A4 and Penrose P1-P2 tilings).

Ammann bars form, in the case of Penrose P2 tiling, a set of 5 regular grids across the tiles which are rotated through 2PI/5 and meet the y axis at different positions.

Architecturally these regular secondary grids across the tiles can be used for panelisation of tiles or lines of structural support.

Sets of Ammann bars can be used to represent and in some sense generate aperiodic tilings because certain intersection configurations give rise to particular vertex neighbourhoods. These in turn can force the placement of other tiles often remote from the original and continuing infinitely across the plane.


Misaligned Ammann bars give rise to tiling holes, that is patches in which it is not possible to place tiles with the necessary matching rules.

Musical Sequences

Ammann bars also form so called musical sequences. The spacing between bars is either long or short. In these musical sequences a short cannot follow a short and a long cannot follow two longs. This is summarised in the following state diagram. The black dots represent decisions with the first decision represented at the top of the diagram, whether to use S (small) or L1 (first large). The next and only other decision is whether to use S or L2 (second large).

When tilings are inflated the new short interval is equal to the old long one and the new long interval is equal to the old long one plus the old short one.

Giving the following substitutions  S’ = L  and  L’ = L + S

Hence the golden ratio   L / S = (L + S) / L ≡  φ

Composed tilings give rise to a further musical sequence by dividing the long intervals of the original tiling. Of course decomposition can be achieved by replacing each short by one new long and replacing each long by one new long and one new short.

The relationship of musical sequences to irrational numbers and the projection of  2D aperiodic tilings from 4D dimensional space is further dealt with in the post “Quasicrystals”.

An Einstein

Recently a single aperiodic tile, an Einstein, has been proposed (Socolar and Taylor, 2011).

With its isolated parts this violates the assumption that prototiles should be topological disks. However it is suggested that this objection can be overcome by connecting the isolated parts in 3D.

Girih Tilings

Girih tiling using geometric star and polygon designs or strapwork is a common feature of Medieval Islamic design. The conventional view is that it they were conceived as a network of zigzag lines drawn directly with straightedge and compass.

Lui and Steinhardt (Lui and Steinhardt 2007) show that by 1200 C.E. a conceptual breakthrough had taken place and girih patterns became thought of as tessellations by a set of equilateral polygons (“girih tiles”) decorated with lines.

The lines enabled the creation of increasingly complex periodic girih patterns. They suggest that by the 15th century these complex patterns combined with self-similar transformations led to the construction of near perfect quasi-crystalline Penrose patterns, five centuries before their discovery in the West.

V+A Spiral Project

Aperiodic tiles were used by Daniel Libeskind and Cecil Balmond in their Victoria and Albert Museum “Spiral” proposal.

Ammann A2 tilings were used in a hierarchical fractal manner at different scales for physical surface treatments, tiles and panels. Ammann bars, enforcing aperiodicity, provided a linear support structure.

The use of aperiodic tiles in this project is well covered in “Informal” (Belmond and Smith, 2007) including this quote from Cecil Belmond (as formatted by him).

“The first shapes that came to mind were distorted pentagons, setting up

craggy and spiked patterns, but they seemed too violent and

‘one dimensional’, not quite in resonance with the Spiral itself.

As the research continued the pattern became more intricate; the

answers seemed to lie in a mathematical mosaic.

We came across a fascinating idea from an American

mathematician called Robert Ammann, He discovered a ‘unit’ of tiling,

of three different interlocking but related shapes-the tiles had a

special and subtle property, each one made up of the other two shapes along

with a reduced version of itself. They fitted according to a set of

exact rules.

Though the pattern produced by these tiles looks similar, the

pattern never repeats: it is aperiodic.”

Bibliography

Grünbaum B., Shephard G. C. (1987)
Tilings and Patterns
W.H. Freeman and Company
New York
 
Socolar J.E.S, Taylor J.M. (2111)
An Aperiodic Hexagonal Tile
Journal of Combinatorial Theory
Series A 118 (2011) pp 2207-2231
arXiv:1003,4279
 
Lui P. J. and Steinhardt P. J. (2007)
Decagonal and Quasi-Crystalline Tilings inMedieval Islamic Architecture
Science Vol 315 Pages 1106-1110
 
Belmond C., Smith J. (2007)
Informal, Pages 189-264
Prestel Munich, Berlin, London, New York
 
 
Posted in Aperiodic Tiling, Architecture, Geometry | Tagged , , | 6 Comments

Periodic and Non-Periodic Tiling

Posted on October 12, 2012 by Graham Shawcross

The concepts of periodic and non-periodic tiling are defined so as to clearly distinguish them from aperiodic tiling; the subject of a future post “Aperiodic Tiling”.

Informally a tiling (of the 2D Euclidean plane) is a collection of subsets of the plane (prototiles) that cover the plane without any gaps or overlapping.

Usually  prototiles are required to be topological disks, that is not to have holes or isolated parts.

Periodic Tiling

Only three regular polygons tile the plane; equilateral triangles, squares and hexagons.

As can be seen triangles and squares have strips that can slide in one direction but hexagons are fixed and unable to slide. Because of this only the hexagonal tiling is truly periodic whilst the triangular and square tilings are more properly described as non-periodic because they admit a potentially infinite number of tilings.

There is a proof that no convex polygon of more than six sides can tile the plane.

Triangles and Quadrilaterals

All triangles tile the plane by trivially converting to quadrilaterals, and all quadrilaterals tile the plane including concave ones .

Quadrilaterals are the basis of lattices (translation in 2 directions)

Pentagons

There are 14 types of convex pentagonal tiling (so far), but no proof that this is the total number possible.  Each type is assumed to have corners A, B, C, D and E with edges a, b, c, d and e with edge a being between corners E and A etc.

With the exception of Type 14, each type is really a small family of shapes that satisfy the specified angular and edge restraints. Type 14 is a unique shape, in that all its angles are determined and all its edges are in fixed ratio.

Hexagons

There are just 3 types of convex hexagonal tiling, with the following specifications:-

Type 1:      A + B + C = 180°,     a = d

Type 2:      A + B + D = 360°,     a = d,     c = e

Type 3:      A = C = E = 120°,      a = b,     c = d,     e = f

Polygons in General

This is the Conway Criterion for general polygonal periodic tiling without reflection

Two opposite edges a and d are parallel, congruent and in same orientation. Each of the other edges b, c, e and f are centrosymmetric (unaltered by 1800 rotation). Most architects probably have some intuitively vague knowledge  of this relationship.

Non-Periodic Tiling

Non-periodic tilings tile the plane in a non-repeating manner but can also tile it in a regular periodic manner. They can be arrived at in a number of different ways:-

Division of Periodic Tiling                           Radial                                     Displaced Radial

Substitution of the triangles by congruent symmetric curves can give apparently more complex tilings.

The substitution can even be 3 dimensional as here of a regular square tiling.

Thomas Hetherwick Studio, Great Ormond Street Hospital.

Whilst these tilings are all irregular in some way they are non-periodic rather that aperiodic because they also permit a regular tiling of the plane. The triangles that make up the radial tilings for instance could also tile the plane in a periodic fashion.

Posted in Aperiodic Tiling, Architecture, Geometry, Tiling | Tagged , , , | 4 Comments

The Container for The Thing Contained

Posted on July 11, 2012 by Graham Shawcross

This post is the result of a recent first visit to Berlin; and in particular to the Altes, Neues and Jüdiches Museums there. These irreverently brought to mind James Thurber’s story Here Lies Miss Groby and her concept of the Container for the Thing Contained, explained as an example of a particular type of metonym. James Thurber (1942)

The real pretext of the story is the old joke

           ” A: What’s your head all bandaged up for?

             B: I got hit with some tomatoes.

             A: How could that bruise you so bad?

             B: These tomatoes were in a can.”

Inverting the concept into The Thing Contained for the Container.

These three museums all have interesting and different relationships between the artefacts they display and the buildings that contain them. In each case this effects the way the observer perceives the artefacts.

Although un-planned the museums were visited in the order they were built.

Karl Friedrich Schinkel’s neo-classical Altes Museum was built as the Royal Museum (1823-30). It was damaged during the Second World War and restored in clean white-walled museum style (1951-66). The two-storey layout is very easy to navigate with a very imposing central circular, dark Pantheon type space, the dome of which is hidden externally so as not to detract from the nearby original Dom building.

The museum houses a collection of Classical Greek, Hellenistic, Roman and Etruscan Statues and related objects that are displayed in a straightforward manner within white walls and blinds. Statues are on simple plinths and are actually touchable. Other objects are in simple glass cases with smaller items such as coins being displayed in adjacent smaller rooms. The effect is of objects that are in a visually harmonious relationship with their environment.

The container complements the contents.

The 19th century neo-classic Neues Museum (1843-55) was designed by Friedrich August Stüler (one of Schinkel’s students). It was severely damaged during the Second World War and reopened in 2009 after radical restoration by David Chipperfield Architects in collaboration with Julian Harrap.

“The design focused on repairing and restoring the original volume, respecting the historical structure.  Both the restoration and repair of the existing is driven by the idea that the original structure should be emphasized in its spatial context and original materiality – the new reflects the lost without imitating it.”

The restoration conforms carefully to the Venice Charter, ICMOS (1964), incorporating each of the building’s individual parts, some still largely intact, others substantially damaged. Missing sections have been repaired and supplemented with new parts as required. The original building had many technical innovations such as the early use of cast iron and the effect of the restoration is in many ways an excavation and exposition of building techniques with a resultant strong materiality.

The museum houses Egyptian and pre-historic objects as it did before the war. A few standout objects such as the head of Nefertiti are beautifully presented. However probably because the restored building is so materially and visually overpowering the objects are nearly all housed in standardised glass enclosures with obtrusive black frames.

The use of these heavy cabinets is probably an attempt to instil some internal coherence to the museum but the overall effect is visually chaotic, and the apparently random positioning of the cabinets does not help.

The container overshadows the contents

To most architects the Jüdiches Museum Berlin means its Daniel Libeskind Building but this is actually an extension to the original baroque museum that was closed in 1933. The old museum was remodelled in 1963-69 as the Museum of Berlin and Daniel Libeskind began a third remodelling in 1993 to create the current museum.

The museum was opened in September 2001 but the Libeskind Building had been opened as an empty building for two years before that, when it attracted great attention and 35,000 visitors. In 2007 Libeskind added an elegant but well-mannered glazed courtyard to the Old Museum Building.

The still empty parts of the Libeskind Building are extraordinarily moving particularly the three axes of the building around which it is organised.

A sloping Axis of Emigration leads through a large glazed but unmarked door to an exterior Garden of Exile. This consists of 49 closely packed square concrete blocks topped with willow trees. This is similar in concept to Peter Eisenmann’s 2006 Memorial to the Jews of Europe that has 2,711 closely packed coffin shaped concrete stelae.

An Axis of the Holocaust leads through another unmarked and forbidding door to the Holocaust Tower. This is a chilling, small, unheated tapering chimney of a space dimly lit from high above. However during our visit to an otherwise busy museum we were the only people we saw entering this space.

Finally an Axis of Continuity leads up through successive flights of stairs, to the permanent exhibition spaces. The last flight is a flight to nowhere, leading rather troublingly to a blank wall, odd for an Axis of Continuity or just ironic.

View down the Axis of Continuity

The positioning of the narrow slit windows of the building follow a precise matrix formed by plotting the addresses of Jewish families on a map of pre-war Berlin and joining the points to form what Libeskind called an “irrational and invisible matrix”. The language, form and geometry of the building are based on this matrix.

It is in its relation, or lack of relation, to this matrix that the permanent exhibition falls down. The really fascinating exhibits are displayed in regular accessible museum fashion with display panels that obscure slit windows and generally disrespect the building and its organising matrix.

The contents are rejecting the container.

I wonder if it wouldn’t have been better for the majority of the permanent exhibition to be housed in the Old Museum particularly the pre Holocaust material. This would allow each building to reflect its own content and powerfully reinforce its meaning.

Several other things gave this wartime child a faintly uncomfortable feeling.

The entrance to the Museum is through the original doorway of the Old Museum under the Prussian national coat of arms flanked by allegorical figures of wisdom and justice showing its original function as a court.

The trees have also been allowed to grow in front of and partly obscure the Libeskind Building from the main street and there is a large fence and row of poplar trees between it and the garden beyond the glazed courtyard.

Together with the fairly unsympathetic installation of the museum exhibits there is just a suspicion that the post-modern part of the museum is somehow unloved.

Bibilography

Thurber, J. (1942)
                          Here Lies Miss Groby
                          The New Yorker
                          March 21 1942 p 14
 
Thurber, J. (1954)
                        Here Lies Miss Groby
                        The Thurber Carnival p 75
                        Penguin Books
                        Harmonsworth
 
ICMOS (1964)
                         IInd International Congress of Architects and
                        Technicians of Historic Monuments
                        Venice.
Posted in Aesthetics, Architecture | Tagged , | 5 Comments

Haptic Bedside Lamp

Posted on June 4, 2012 by Graham Shawcross

I had surprisingly forgotten about this haptic lamp that actually sits in one of our bedrooms. We originally came across them in a smart B+B in Arboyne and initially were flumoxed by them.

Haptic Lamp in Off position

Haptic Lamp in On position

The clue to its use is on the label that says <-On-Off->

Haptic nature revealed by the fact that the lamp can be easily operated with one hand in the dark.

Posted in Design, Geometry, Haptic Objects, Products | Tagged , , , | 3 Comments

Abbott Thayer, Countershading and Camouflage Theory

Posted on May 31, 2012 by Graham Shawcross

This gallery contains 11 photos.

Abbott Handerson Thayer (1849-1921) was for a time one of America’s most famous portrait painters. He was also an accomplished painter of the natural world, being particularly interested in animal colouration. He made three important contributions to camouflage theory. These … Continue reading →

More Galleries | Tagged , | 2 Comments

Haptic Radios

Posted on May 17, 2012 by Graham Shawcross

Radios that can be operated in the dark with one hand.

Version 1

Battery in square enclosure acts as on-off switch, programme selector, volume control and power supply.

No buttons, dials, sliders or other moving parts.

Because radio can be operated in the dark, all parts can be transparent.

Simple construction, electronic components all on simple base board.

Version 2

Version 2

Battery in circular container controls on-off and station by pushing in and releasing. Volume is controlled by rotating battery.

More compact than Version 1 but a little more difficult to operate with one hand.

Posted in Design, Haptic Objects, Products | Tagged , | 3 Comments

Thawing Frozen Music

Posted on April 30, 2012 by Graham Shawcross

Goethe is usually credited with using the phrase “I call architecture frozen music” in a letter published in 1836. (Eckermann 1836)

A similar phrase “Architecture is like frozen music” seems to have been used earlier in Schelling’s Philosophy of Art. (Schelling 1802-03)

Inversely sound can be made visible in a number of ways.

Chladni Patterns are generated by putting fine sand on a metal plate and vibrating it usually with a violin bow. The patterns occur in locations where there is least movement and the fine sand accumulates.

They can also be generated artificially as 3D surfaces.

Xenakis

Peter Nelson recently gave a seminar in the French Department on Iannis Xenakis with whom he had worked in Paris.

Xenakis was the architect, with Le Corbusier, of the Philip’s Pavilion at Expo 58 in Brussels.

Edgard Varèse’s Poème électronique was performed at the opening of the pavilion :-

http://www.youtube.com/watch?v=WQKyYmU2tPg

Xenakis gave up architecture to devote himself to the composition of electronic music and the development of his UPIC system (Unite Polyagogique Informatique de CEMAMu) .

There are fairly obvious visual connections between the hyperbolic form of the Philip’s Pavilion and Xenakis’s method of representing Glissandi above.

An excerpt of Xenakis using UPIC can be seen and heard here

http://www.youtube.com/watch?v=7_Gu0qDAys0

An example of UPIC playing an elevational drawing of  Corbusier’s Ronchamp is illustrated below; an example of frozen music being thawed.

Drawing and sound work together, the visual cursor prepares an expectation of the sound because it is possible to look ahead and anticipate.

It can be heard and seen  in the link below, and the sound expectations that the moving red cursor gives appreciated.

http://cargocollective.com/tommasonervegna/Xenian-Project

Xenakis was the author of the monumental, Formalised Music: Thought and Mathematics in Composition, (Xenakis 2001) which does not seem to have an architectural equivalent.

The day after Peter Nelson’s seminar I accidentally came across a program called IanniX on a departmental machine (ianniX.com).

This is readily available and seems to be an updated version of UPIC developed under the auspices of the French Ministry of Culture. It avoids the use of a digitiser, reminiscent of old CAD systems, and produces Open Sound Control (OSC) events and curves.

Before I heard UPIC play the Ronchamp drawing I thought it would be interesting to modify an existing  animation program to produce music.

Separate Modelling and Viewing

Given that well designed CAD and animation programs carefully separate modelling and viewing it should be possible to see modelling as musical composition and viewing as playing the model.

Modelling –> Composition

Define volumes, shapes and material properties varying over time.

Viewing –> Playing

Where the viewing plane cuts the model at a particular place and time produces a, possibly  moving, 2D image that sound can be generated from. That is the viewing plane can be treated like the line cursor in UPIC. There could be many playings of the same model produced on different physical devices. Each view could also be modified to respond to the model in specific ways analogous to individual instruments.

Playing(s) –> Sound Console –> Conducing

Many individual playings could be collected into a performance controlled by a conductor.

Besides having models specifically designed as musical compositions it would be possible to play 3D models representing buildings either known pieces of architecture or as a means of ‘hearing’ a proposed design.

Experiencing architecture is also analogous to this process. A design is developed,  built and hopefully maintained over time; whilst a multitude of viewers with different interests examine and visit it at different times.

Bibliography

EckerMann, J. P. (1836)  Conversations with Goethe
                             trans Oxenford, J.(1906)
                            Harrison Ainsworth
 
Schilling, F.W.J. (1802-03) Philosophie der Kunst
                            The Philosophy of Art (1989)
                            Minnesota University Press
 
Xenakis, I. (2001)
                            Formalised Music: Thought and Mathematics in Composition
                            (Harmonologia Series No.6)
                            Pendragon Press
 
 
Posted in Architecture, Frozen Music | Tagged , , , | 1 Comment

Quasicrystals and Aperiodic Tiling

Posted on April 26, 2012 by Graham Shawcross

In 2011 Dan Shechtman was alone awarded the Nobel Prize in Chemistry for the discovery of quasicrystals.

Shechtman found in 1982 that atoms in a crystal could exhibit 5 fold symmetry packed in a pattern that did not repeat itself; analogous to aperiodic tiling in 2 dimensions.

He was ridiculed because this result contradicted accepted crystallographic theory.

The head of his research group told him to “go back and read the textbook” and then asked him to leave his research group for ‘bringing disgrace’ on the team.

Shechtman then experienced several years of hostility; Linus Pauling even said “There is no such thing as quasicrystals, only quasi-scientists.” (Hargittai 2011)

Up until now there have not been many practical applications of quasicrystals, but hard steel quasicrystals embedded in softer steel are used in some razor blades and in some thin needles used in eye surgery.

Marjorie Senechal in Quasicrystals and Geometry (Senechal 1996) says that

 “Increasingly, mathematicians and physicists are becoming intrigued by the quasicrystal phenomenon, and the result has been an exponential growth in the literature on the geometry of diffraction patterns, the behaviour of the Fibonacci and other non periodic sequences, and the fascinating properties of the Penrose tilings and their many relatives.”

Marjorie Senechal gave the following lecture at a Special Symposium on Quasicrystals Honoring Distinguished Prof. Danny Shechtman on his 70th Birthday titled:-

“What Quasicrystals have done for Mathematics”

http://www.youtube.com/watch?v=pjao3H4z7-g

Her main argument is that the discovery of quasicrystals has encouraged mathematicians to think visually again. In this respect she also gives credit to Martin Jay’s Downcast Eyes: The Denigration Of Vision In Twentieth-Century French Thought, (Jay 1994).

Claude Bragdon gives an early historical perspective on projective geometry but to my mind heavily tainted with Astral Planes and Theosophy. (Loftus 1999)

Tony Robbin, (Robbin 2006) gives a less tainted view of the projection of aperiodic tiling from higher dimensional models

In particular he shows how aperiodic Penrose tiling can be projected from 4 dimensional models, and gives a 2 dimensional example of how the projective method works.

This shows the relation of irrational numbers to so called musical sequences and thence to Penrose Tiling.

In musical sequences a long interval can follow another long interval but a short interval must follow two long intervals, and a short interval must be followed by a long one.

When inflated the new short interval is equal to the old long interval and the new long interval is equal to the length of the old long interval plus the old short interval.

Giving the following substitutions  S’ = L  and  L’ = L + S

Hence the golden ratio   L / S = (L + S) / L ≡  φ

Continuous inflation or composition proves the ability of aperiodic tiling to cover the plane. The substitutions are also suitable for L-System application.

The interactive program called Quasi Tiler produces outputs like that shown below, it shows the 4 dimensional structure and the Penrose  aperiodic tiling generated by projection from it

A fairly full description of the program is available at http://www.geom.uiuc.edu/apps/quasitiler/about.html#conclusion

The program is not currently working but source code is available and could be resurrected at the price of learning Java.

Bibliography

Loftus, S (1999)
                       Claude Bragdon in Context
                       Edinburgh Architectural Research Volume 26  
 
Jay, M (1994)
                        Downcast Eyes:
                        The Denigration of Vision in Twentieth-Century French Thought
                        The University of California Press
 
Hargittai, I. (2011)
                        ‘There is no such animal’—Lessons of a Discovery
                        Structural Chemistry (2011) 22:745-748
 
 Senechal, M. (1996)
                        Quasicrystals and Geometry
                        Cambridge University Press
 
Robbin, T.(2006)
                        Shadows of Reality:
                        The Fourth Dimension in Relativity, Cubism and Modern Thought.
                        Yale University Press
Posted in Aperiodic Tiling, Geometry | Tagged , | 2 Comments