This closely follows “Tilings and Patterns” (Grünbaum and Shephard, 1987), but uses coloured diagrams rather than their monochrome ones. In some ways this is simply a catalogue of aperiodic tilings, their various forms and some indication of their uses, but my interest comes from their ability to be at the same time both regular in form, and random in distribution.

Aperiodic tiling can only tile the plane in a non-repeating manner. This is in contrast to non-periodic tiling that can tile the plane in an irregular manner but can also do so in a regular, periodic fashion.

Aperiodic tilings often requires that tile edges be marked, coloured or keyed in some way to force aperiodicity, and a number of examples are illustrated below.

Aperiodic Tilings are usually named for their originators, there are Wang, Robinson, Ammann and Penrose tilings. Where an originator has more than one tiling to their name these are designated as follows Ammann A2 tiling, Penrose P3 tiling etc.

Wang Tiling

Wang tiles consist of square tiles with coloured edges, which must be placed edge-to-edge. They tile the plane following the rule that adjacent tiles must have matching edge colours. Rotation or reflection of tiles is not allowed.

The tiles above can also be coloured as follows:-

With physical tiles the prohibition on rotation can be enforced by a trivial shape modification:-

The matching conditions (colours) can also be represented by numbers, as is done in “Tilings and Patterns”  (Grünbaum and Shephard, 1987).

Wang tiles can be used to mimic any Turing Machine where rows of tiles simulate consecutive states of the machine, this is the subject of a separate post, “Wang Tiles and Turing Machines”.

Methods have been developed that use the other aperiodic tilings to generate very small sets of Wang tiles and these are described in another post, “Wang Tiles and Aperiodic Tiling”.

Wang tile sets are usually described by the number of tiles in the set together with the number of different edge colours used, for example 13 tiles over 5 colours. This is currently the smallest known set.

Other Aperiodic Tilings

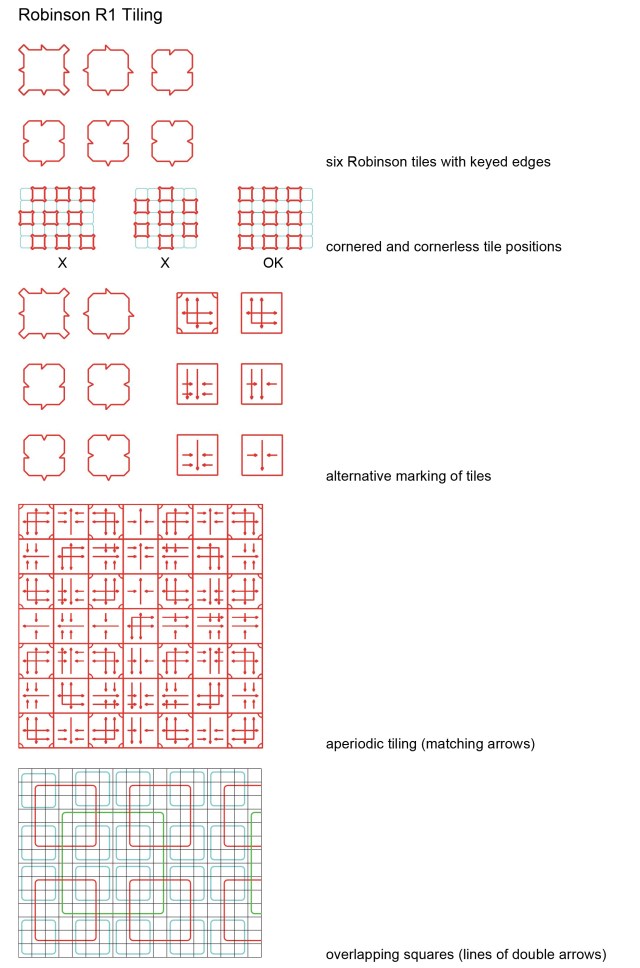
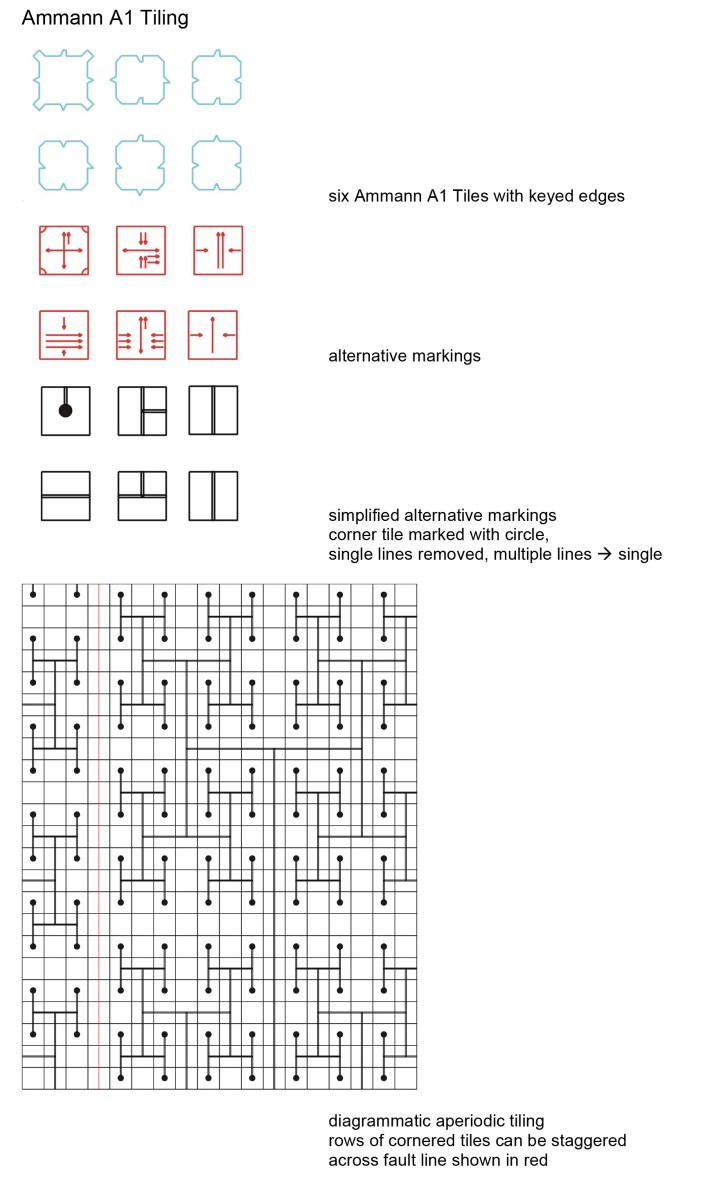
Robinson R1 and Ammann A1 tilings are both similar, using square tiles with keyed edges.

 

 

Ammann Bars

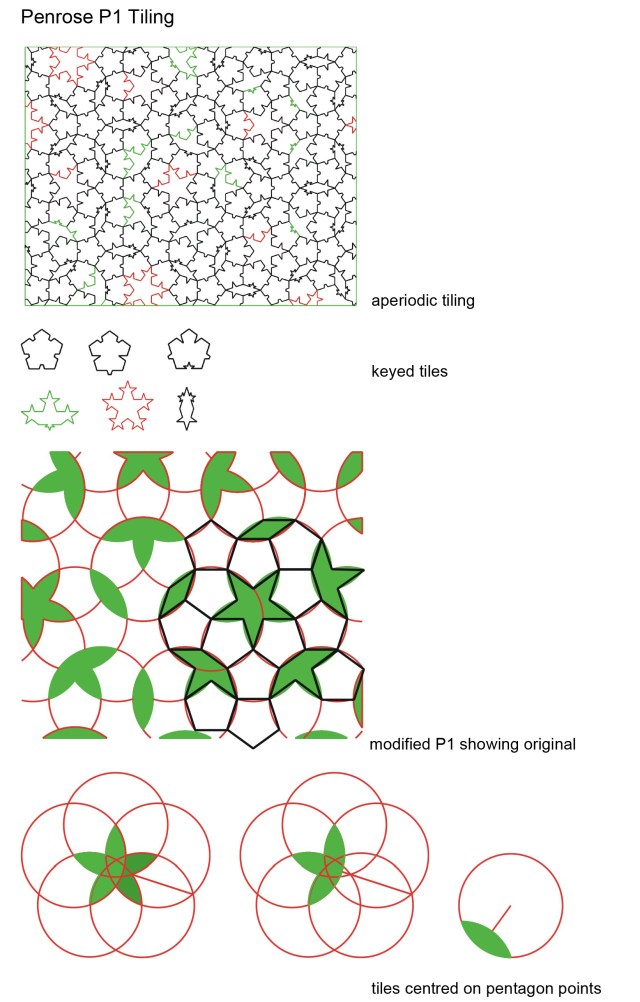
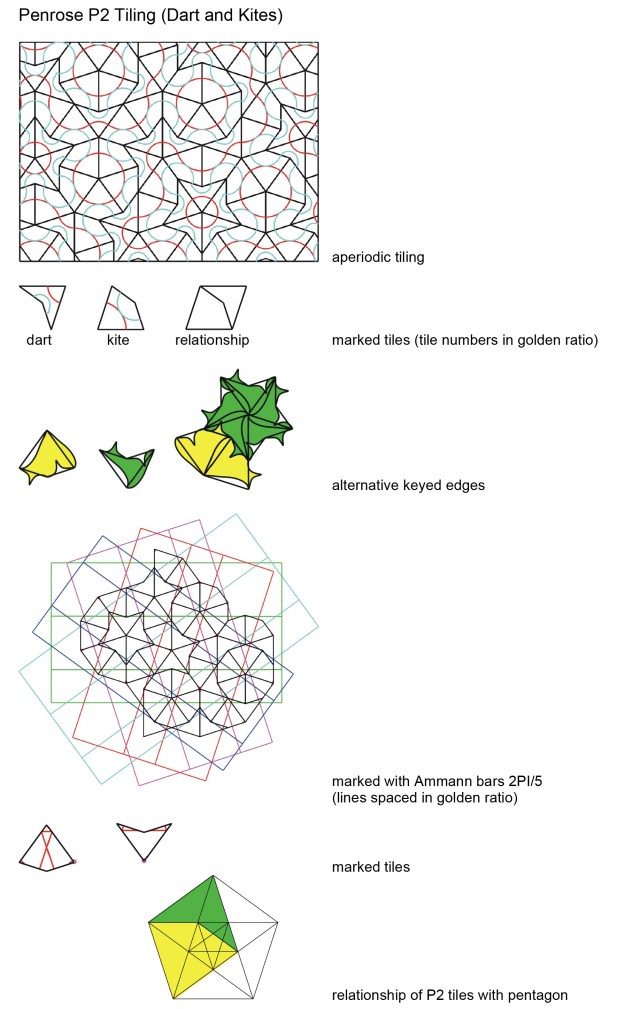
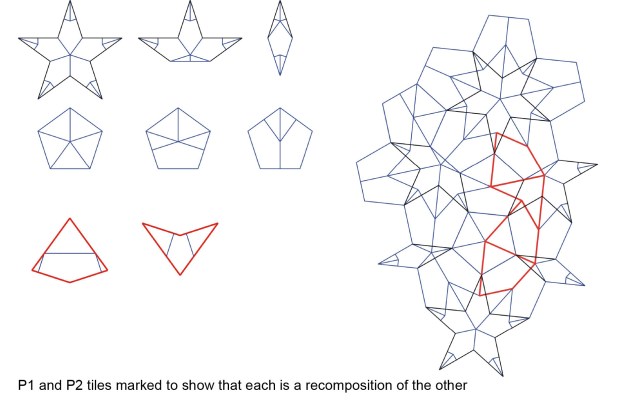
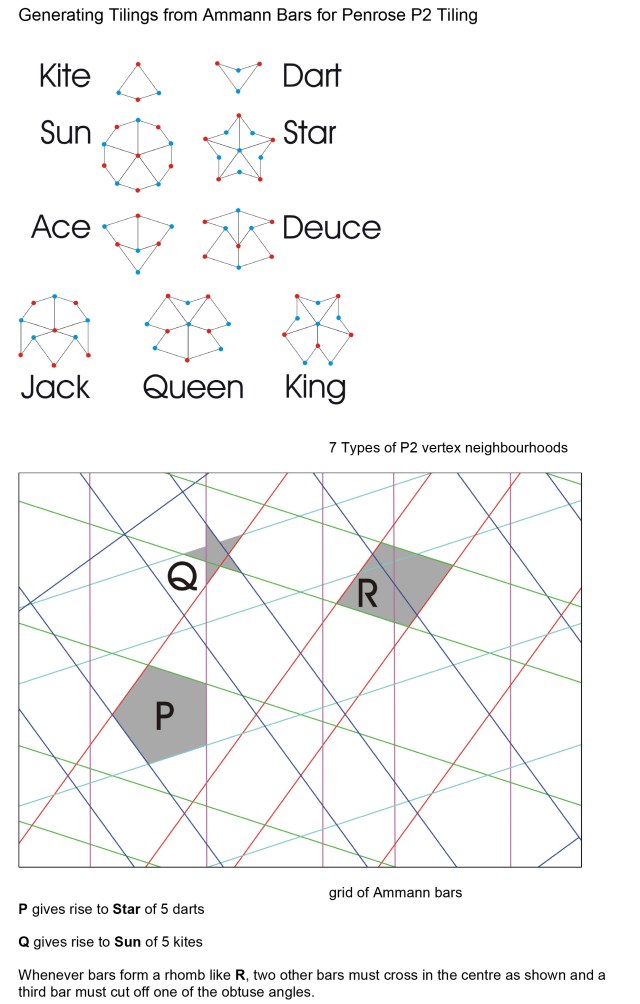
Robert Ammann proposed the use of linear markings (Ammann bars) to enforce aperiodicity on tile sets. This is achieved by requiring that the bars on adjacent tiles line through. These have been indicated on many of the tilings above, (the Ammann A1-A4 and Penrose P1-P2 tilings).

Ammann bars form, in the case of Penrose P2 tiling, a set of 5 regular grids across the tiles which are rotated through 2PI/5 and meet the y axis at different positions.

Architecturally these regular secondary grids across the tiles can be used for panelisation of tiles or lines of structural support.

Sets of Ammann bars can be used to represent and in some sense generate aperiodic tilings because certain intersection configurations give rise to particular vertex neighbourhoods. These in turn can force the placement of other tiles often remote from the original and continuing infinitely across the plane.

Misaligned Ammann bars give rise to tiling holes, that is patches in which it is not possible to place tiles with the necessary matching rules.

Musical Sequences

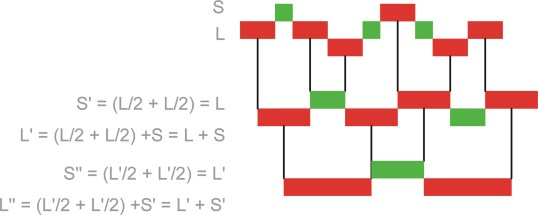
Ammann bars also form so called musical sequences. The spacing between bars is either long or short. In these musical sequences a short cannot follow a short and a long cannot follow two longs. This is summarised in the following state diagram. The black dots represent decisions with the first decision represented at the top of the diagram, whether to use S (small) or L1 (first large). The next and only other decision is whether to use S or L2 (second large).

When tilings are inflated the new short interval is equal to the old long one and the new long interval is equal to the old long one plus the old short one.

Giving the following substitutions  S’ = L  and  L’ = L + S

Hence the golden ratio   L / S = (L + S) / L ≡  φ

Composed tilings give rise to a further musical sequence by dividing the long intervals of the original tiling. Of course decomposition can be achieved by replacing each short by one new long and replacing each long by one new long and one new short.

The relationship of musical sequences to irrational numbers and the projection of  2D aperiodic tilings from 4D dimensional space is further dealt with in the post “Quasicrystals”.

An Einstein

Recently a single aperiodic tile, an Einstein, has been proposed (Socolar and Taylor, 2011).

With its isolated parts this violates the assumption that prototiles should be topological disks. However it is suggested that this objection can be overcome by connecting the isolated parts in 3D.

Girih Tilings

Girih tiling using geometric star and polygon designs or strapwork is a common feature of Medieval Islamic design. The conventional view is that it they were conceived as a network of zigzag lines drawn directly with straightedge and compass.

Lui and Steinhardt (Lui and Steinhardt 2007) show that by 1200 C.E. a conceptual breakthrough had taken place and girih patterns became thought of as tessellations by a set of equilateral polygons (“girih tiles”) decorated with lines.

The lines enabled the creation of increasingly complex periodic girih patterns. They suggest that by the 15th century these complex patterns combined with self-similar transformations led to the construction of near perfect quasi-crystalline Penrose patterns, five centuries before their discovery in the West.

V+A Spiral Project

Aperiodic tiles were used by Daniel Libeskind and Cecil Balmond in their Victoria and Albert Museum “Spiral” proposal.

Ammann A2 tilings were used in a hierarchical fractal manner at different scales for physical surface treatments, tiles and panels. Ammann bars, enforcing aperiodicity, provided a linear support structure.

The use of aperiodic tiles in this project is well covered in “Informal” (Belmond and Smith, 2007) including this quote from Cecil Belmond (as formatted by him).

“The first shapes that came to mind were distorted pentagons, setting up

craggy and spiked patterns, but they seemed too violent and

‘one dimensional’, not quite in resonance with the Spiral itself.

As the research continued the pattern became more intricate; the

answers seemed to lie in a mathematical mosaic.

We came across a fascinating idea from an American

mathematician called Robert Ammann, He discovered a ‘unit’ of tiling,

of three different interlocking but related shapes-the tiles had a

special and subtle property, each one made up of the other two shapes along

with a reduced version of itself. They fitted according to a set of

exact rules.

Though the pattern produced by these tiles looks similar, the

pattern never repeats: it is aperiodic.”

Bibliography

Grünbaum B., Shephard G. C. (1987)

Tilings and Patterns

W.H. Freeman and Company

New York

 

Socolar J.E.S, Taylor J.M. (2111)

An Aperiodic Hexagonal Tile

Journal of Combinatorial Theory

Series A 118 (2011) pp 2207-2231

arXiv:1003,4279

 

Lui P. J. and Steinhardt P. J. (2007)

Decagonal and Quasi-Crystalline Tilings inMedieval Islamic Architecture

Science Vol 315 Pages 1106-1110

 

Belmond C., Smith J. (2007)

Informal, Pages 189-264

Prestel Munich, Berlin, London, New York