Written and spoken numbers are represented differently. In English numbers are usually written with Arabic numerals or as a transliteration of the spoken version, for example 342 or three hundred and forty two.

Rod counting provides a written representation of number and a mechanical calculating process that like the abacus takes advantage of the subitising effect, the ability to just glance at a small group of objects and without effort be immediately aware of how many objects are in the group.

For more details of  subitising see https://grahamshawcross.com/2014/01/09/subitising/

Hybrid Addition and Multiplication

Verbal numbers, the way numbers are spoken, in English are organised as a hybrid series of additions and multiplications summarised, for the number 350172, by the graph below where the plus signs indicate addition and the X signs multiplication.

After Dehaene (1992) Varieties of Numerical Abilities Cognition, 44 1-42

So that ((((three is multiplied by a hundred) and added to fifty) which is then multiplied by a thousand) and added to ((one multiplied by a hundred) added to (seventy added to two)))

This system involves a combination of simple number words; one, two, three etc., some special multiplier words like hundred, thousand etc and the particularly English -ty words like twenty, thirty, seventy etc and -teen words like thirteen, fourteen etc. plus the unique eleven and twelve.

With Arabic numerals the same number (350172) is represented positionally; starting with the rightmost numeral being the quantity of units (2) and the next leftward numeral being the quantity of tens (7) etc. Note that Arabic numbers are read, or more accurately generated, from right to left, perhaps betraying their origin.

Literate English speakers have no problem reading, writing, comprehending or producing both systems and transcoding between them even though there is evidence, through the study of patients with deficits in one or more of these capacities, of a neurological dissociation of the two systems. (McConey 1992)

Tally Marks

Tally marks are the simplest unary form of number system. To count n items or events one simply makes n marks. Tally marks are best suited to counting and recording continuing sequences, for example, counting flocks of animals or scores from a game. They are very simple to implement with scratching, sticks, pencil or chalk marks and occur with slight variations in many cultures.

In the top row, marks just continue to be added one after another, but in the other rows the marks are collected into groups of five by various methods. These include using the fifth mark of a group to strike through the previous four marks (second and third row) and drawing the first or last member of a group at a slope (fourth and fifth row).

Collecting the tallies into equal sized groups as you count helps avoid errors and groups of five make counting effortless and eases later conversion into decimal notation. Simple arithmetic such as addition and subtraction can easily be carried out between two sets of tallies.

Chinese Rod Numerals

Zero in both orientations is just represented by a space, which conveniently has no colour so is neither positive or negative.

Taking advantage of the subitising effect, a small number of rods or sticks, at most 5, are used to make up all the necessary 1 to 9 numerals with the form changed (one stick rotated) after 5 rods have been used in tally mark fashion. So the rotated rod represents 5 units and the numeral 6 is represented by one rotated rod plus one un-rotated rod (5 + 1) and the numeral 7 by one rotated rod plus two un-rotated rods (5 + 2) etc. If the rotated rod was introduced at numeral 5, it would just be a single rotated rod and be indistinguishable from the alternative, horizontal or vertical, version of numeral 1. So a rotated rod is first used for numeral 6 where it appears with 1 un-rotated rod. This is to preserve an essential property of any number system, being able to represent all possible numbers unambiguously.

Positional Representation

As with Arabic numbers, Chinese Rod numbers use a positional representation starting with the units on the right and proceeding leftwards to the tens, hundreds etc. Below are examples of rod number representing the numbers 231, 5089 and 50089 respectively.

The horizontal and vertical forms of each number are used alternatively to help indicate the position of the numerals starting with the vertical form in the units position, the horizontal form in the tens position etc.

Zeros, represented merely by spaces, can usually be identified by the orientation of adjacent numerals. If adjacent numerals have the same orientation and are somewhat separated, this indicates that there is one, or an odd number of zeros, as in 5089 above. If they are of different orientation and somewhat separated, this indicates that there are two, or an even number of zeros, as in 50089 above.

Two approaches developed for overcoming problems arising from multiple spaces which are obviously error prone. For instance, differentiating between 3 and 5 spaces or between the numbers 50 and 5000 which both have zero in the rightmost units position.

One approach was to use a place marker,  other than a space, for zero; by some accounts, a Go bead or pebble which in later written versions became an open circle like the Indian or Arabic symbol for zero. The example below also shows modifications that reduce the number of strokes required when writing the numerals 4, 5 and 9.

Here 5 is 0 plus a rotated rod and 9 is 4 plus a rotated rod, so the concept of a rotated rod representing 5 has been retained and the first introduction of a rotated rod moved from 6 back to 5. This reintroduces an equal division of the 10 numerals into 2 sets of 5, as with 5 fingers on 2 hands.

The other approach to avoiding problems with zeros was to use a counting grid marked out on a board or cloth.

18th Century Japanese Counting Board

Counting Grids

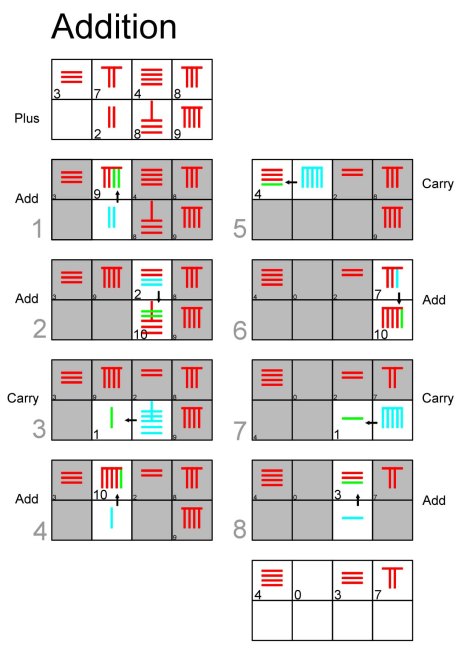
Once the units column has been fixed, perhaps leaving space for tenths and hundredths etc., a counting grid removes all ambiguity with regard to spaces and the representation of zero, and removes the need for horizontal and vertical versions of the numerals. It also allows a wide range of calculations to be carried out by just by moving rods. The moves for addition and subtraction are indicated in order below, with temporally cyan coloured rods being moved to their new green positions and grey rods showing where rods have been removed.

There are also procedures for multiplication, division, square and even cube roots. So calculations can be be carried just by moving objects, a process that is greatly aided by never having to count more than 5 objects in any grid square.

Roman Numbers

The Roman numerals are I (1), V (5), X (10), L (50), C (100), D (500) and M (1000). Roman numbers use a non-positional and essentially additive representation. For instance the number 2014 in Roman numerals is MMXIV with working from left to right MM (2000) added to X (10) added to IV (4).

To avoid needing to use four copies of the same number, I can be placed in front of V or X to represent 4 and 9, replacing IIII and VIIII with IV and IX. In a similar manner X can be placed in front of L or C to give XL (40) and XC (90). C can also be placed in front of D or M to give CD (400) and CM (900). This is a rule or convention that does not need to be observed, for instance on clock faces with Roman numerals where 9 o’clock is always IX but 4 o’clock is often IIII rather than IV probably because its position makes the direction of IV and VI potentially ambiguous.

The non-positional character of Roman numbers can be appreciated by comparing Roman MMXIV (2014) with MCMXCVI (1996) were the smaller number uses more numerals than the larger number.

Roman Calculation

The English word calculation derives from the Latin word calx, plural calculi, the name of the small stones or pebbles used by the Romans for counting and calculating.

In Roman calculation, stones are placed on lines representing units, tens, hundreds and thousands (marked I, X, C and M respectively). The spaces between the lines are used to represent intermediate values that is 5, 50, 500 etc. (that could be marked V, L and D). So it is never necessary to use more than 5 stones on a line or more than 2 stones in a space. This is because 5 stones on a line can be replaced by one stone in the space above and 2 stones in a space can be replaced by one stone on the line above (carrying). Or the reverse a stone in a space can be replaced by 5 stones on the line below or one stone on a line can be replaced by two stones in the space below (borrowing). Zero is simply represented by an empty line or space. This is mathematically equivalent to the Chinese or Japanese abacus and indeed there were Roman abacuses of similar design.

Whilst it appears difficult if not impossible to do calculations using written Roman numerals, the numerals themselves seem eminently appropriate when seen as part of a grid based calculating system. This is particularly so with the, possibly implied, halfway markers V, L and D, representing 5, 50 and 500 respectively, that reduce the need to ever use more than 5 counters.

The use of positional modifiers, IV for 4 and IX for 9 etc, seems to be a latter convention related to the efficient writing of long numbers like dates and do not form a part of the calculating system.

Discussion

The main point of this post is to highlight the ubiquity and utility of the subitising effect, the ability to glance at a small group of objects and without effort be immediately aware of how many objects are in the group.

Number systems are not designed but evolve, so it is difficult to describe their development without being teleological. But one can say that tally marks, grid based calculating systems and abacuses all work well because their moving parts as it were, scratches, rods, stones or beads, never occur in groups of more than 5; that is they always appear in groups that can be easily recognised without conscious effort.

With grid based calculating systems, including abacuses, the moves necessary to do calculations can therefore be carried out without unnecessary effort being expended on explicitly counting the rods, stones or beads. Explicit counting probably means using spatial shifts of attention to identify the objects and the internal use of verbal counting, one, two, three etc. Recognition times for numerals within the subitising range, 1 to 5, are half those for numerals outside the range, that is 6 to 9. This is a difference that a system can evolve to take advantage of.

With Chinese Rod numerals there appears to be a fine tuning, or co-evolution, of the requirement to represent all numbers unambiguously and never have more than 5 elements in any numeral, so the numeral 5 has 5 rods rather than 1 rotated rod which would be indistinguishable from the alternative, horizontal or vertical, numeral 1.

Tally marks have a one to one relationship to the objects or events they are counting and perhaps just as importantly recording. It seems almost unnecessary to call these marks numerals as they operate more like a modern click counter; one just automatically makes a mark probably without any mental counting and can ‘see’ without counting when four marks have been made and a cross mark or slanted line is required. In scoring a game two sets of tallies can be easily compared to see who is winning. Or a further explicit counting process of the grouped tallies can easily be carried out to get an overall numeric total. Collecting marks into groups of  5 therefore satisfies two desiderata; to have effortless counting and easy later conversion to a decimal system should this be wanted.

With Rod Numerals the quantity of rods in a numeral and its value are also matched or related; for instance the numeral 4  has 4 rods and less obviously the numeral 7  has 5 plus 2 rods but importantly only 3 elements. The Roman Numerals I, II, III, IIII etc. also have this relationship and the numerals V and X retain some semblance of sticks or marks. In both cases this relationship could aid the recognition of the numerals or just be a vestigial reminder of their origins. The relationship barely exists with Arabic numerals, except perhaps for the Arabic numeral 1, these numerals having a script based origin rather than being based on collections of physical objects like marks, sticks or stones.

Grid based calculations with Rod Numerals are carried out by moving the actual rods that make up the numerals and essentially transposing pairs of numerals whilst conserving quantity so for instance by moving two rods from  to  you get  and  so (4 + 7) = (2 + 9). A more useful operation would be to move 3 rods to effect a carry so that (4 + 7) = (1 + 10) with the 10 being carried as a 1 into the next leftwards square.

Roman grid based calculation and abacuses do not share this property because numbers are represented by the position and quantity of logically identical stones or beads on the grid or wires. These types of calculation are not restricted to base 10 number systems and can be used with any base, provided that the space between the lines or above and below the abacus beam represents half the base. So in the Roman calculation example the lines record the powers of the base 10; 10⁰ = 1 = I, 10¹ = 10 = X, 10² = 100 = C, 10³ = 1000 = M and the spaces record the values of half the line above; 10¹÷2 = 5 = V, 10²÷2 = 50 = L, 10³÷2 = 500 = D, a pattern that can be used for other bases. With these systems zero is represented without any difficulty or consequences by the lack of a stone on a line or in a space or the fact that no beads have been moved towards the abacus beam.

The widespread, but far from universal, preference for base 10 number systems is usually thought to relate to the use of 10 fingers for counting, a clue being in the word digit, a synonym for numeral, that derives from the Latin digiti meaning fingers. More accurately digits are the glyphs that are used repeatedly in positional number systems, so a base 10 number system requires 10 digits (0 1 2 3 4 5 6 7 8 9) and a binary, base 2, system needs 2 digits (0 1) etc.

Bibliography

Dehaene, S. (1992) Varieties of Numerical Abilities Cognition, 44 1-42

Knuth, D. (1997) The Art of Computer Programming. Volume 2, 3rd Ed. Addison–Wesley. pp. 194–213, “Positional Number Systems”.

McCloskey, M. (1992) Cognitive mechanisms in numerical processing: Evidence from acquired dyscalculia, Cognition 44 107-157

Needham, J. (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.