The concepts of periodic and non-periodic tiling are defined so as to clearly distinguish them from aperiodic tiling; the subject of a future post “Aperiodic Tiling”.

Informally a tiling (of the 2D Euclidean plane) is a collection of subsets of the plane (prototiles) that cover the plane without any gaps or overlapping.

Usually  prototiles are required to be topological disks, that is not to have holes or isolated parts.

Periodic Tiling

Only three regular polygons tile the plane; equilateral triangles, squares and hexagons.

As can be seen triangles and squares have strips that can slide in one direction but hexagons are fixed and unable to slide. Because of this only the hexagonal tiling is truly periodic whilst the triangular and square tilings are more properly described as non-periodic because they admit a potentially infinite number of tilings.

There is a proof that no convex polygon of more than six sides can tile the plane.

Triangles and Quadrilaterals

All triangles tile the plane by trivially converting to quadrilaterals, and all quadrilaterals tile the plane including concave ones .

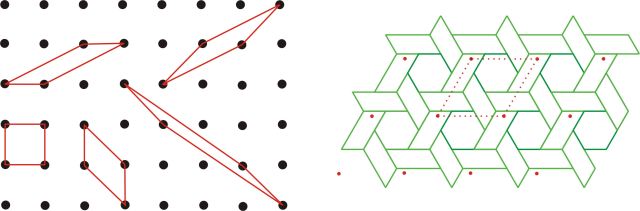
Quadrilaterals are the basis of lattices (translation in 2 directions)

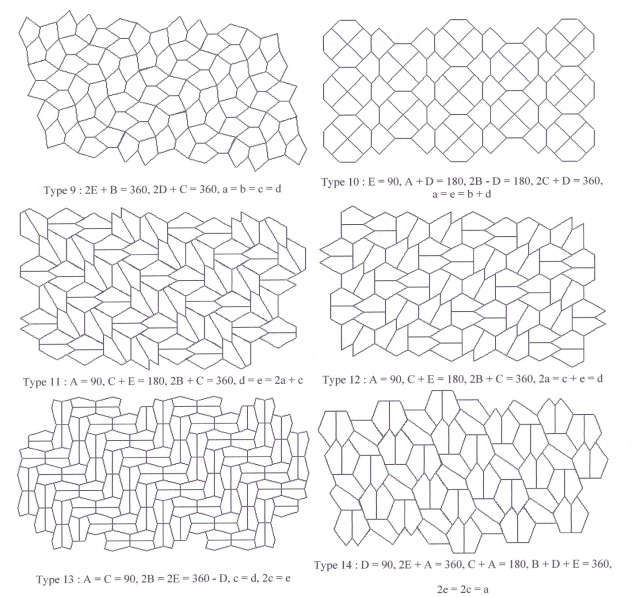
Pentagons

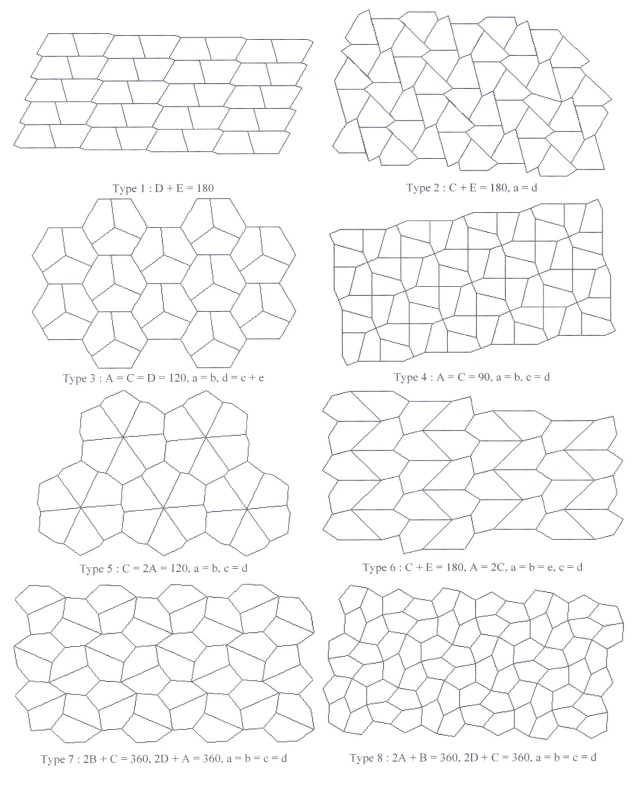
There are 14 types of convex pentagonal tiling (so far), but no proof that this is the total number possible.  Each type is assumed to have corners A, B, C, D and E with edges a, b, c, d and e with edge a being between corners E and A etc.

With the exception of Type 14, each type is really a small family of shapes that satisfy the specified angular and edge restraints. Type 14 is a unique shape, in that all its angles are determined and all its edges are in fixed ratio.

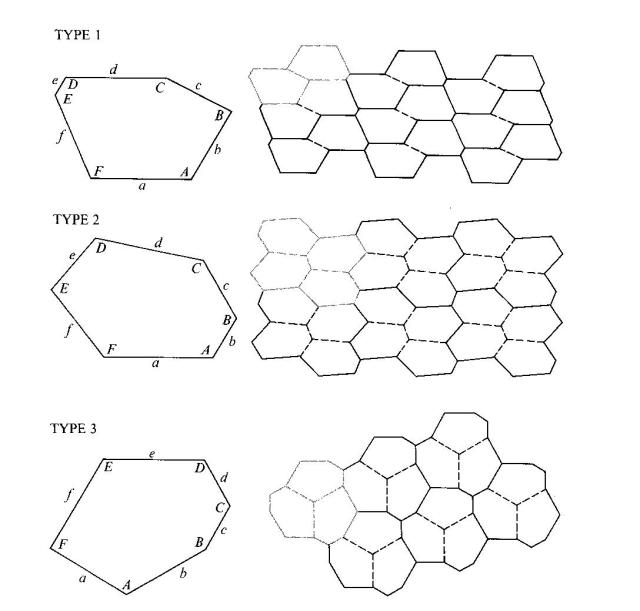
Hexagons

There are just 3 types of convex hexagonal tiling, with the following specifications:-

Type 1:      A + B + C = 180°,     a = d

Type 2:      A + B + D = 360°,     a = d,     c = e

Type 3:      A = C = E = 120°,      a = b,     c = d,     e = f

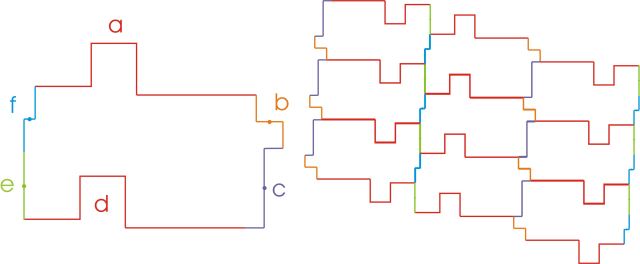
Polygons in General

This is the Conway Criterion for general polygonal periodic tiling without reflection

Two opposite edges a and d are parallel, congruent and in same orientation. Each of the other edges b, c, e and f are centrosymmetric (unaltered by 180⁰ rotation). Most architects probably have some intuitively vague knowledge  of this relationship.

Non-Periodic Tiling

Non-periodic tilings tile the plane in a non-repeating manner but can also tile it in a regular periodic manner. They can be arrived at in a number of different ways:-

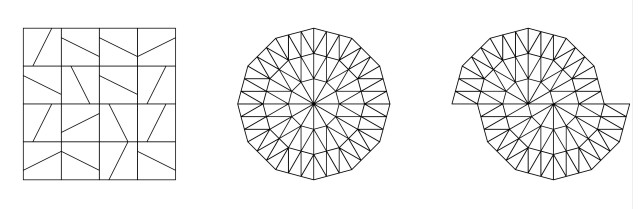Division of Periodic Tiling                           Radial                                     Displaced Radial

Substitution of the triangles by congruent symmetric curves can give apparently more complex tilings.

The substitution can even be 3 dimensional as here of a regular square tiling.

Thomas Hetherwick Studio, Great Ormond Street Hospital.

Whilst these tilings are all irregular in some way they are non-periodic rather that aperiodic because they also permit a regular tiling of the plane. The triangles that make up the radial tilings for instance could also tile the plane in a periodic fashion.