A year-out student Tom Kirby emailed an office of 200 people asking what the convention was for beyond and behind dotted line styles. No one knew. On-line searches didn’t prove very helpful so in one of those mad delightful collective moments it was decided to use Morse Code line styles. We would then be able to put any message we liked as a line, including beyond and behind or the scatological, and no one would be any the wiser.
Note that there are really 3 symbols here, a dot, a dash and a space. The definition of the space between characters and the space between words are also important in defining what is in some ways a modular system.
In AutoCAD line type definitions like this should work (followed by 7 spaces).
*BEYOND,Beyond _… . _.__ ___ _.__ _..
A,12.7, -6.35, 0, -6.35, 0, -6.35, 0, -19.0, 0, -19.0, 12.7, -6.35, 0, -6.35, 12.7, -6.35, 12.7, -19.0, 12.7, -6.35, 12.7, -6.35, 12.7, -19.0, 12.7, -6.35, 0, -6.35, 12.7, -6.35, 12.7, -19.0, 12.7, -6.35, 0, -6.35, 0, -44.5
*BEHIND,Behind _… . … .. _.__ _..
A,12.7, -6.35, 0, -6.35, 0, -6.35, 0, -19.0, 0, -19.0, 0, -6.35, 0, -6.35, 0, -19.0, 0, -6.35, 0, -19.0, 12.7, -6.35, 0, -6.35, 12.7, -6.35, 12.7, -19.0, 12.7, -6.35, 0, -6.35, 0, -44.5
But unfortunately AutoCAD only allows a maximum of 12 dots or dashes, too bad.
Yin and Yang
The I Ching consists essentially of 64 chapters with each chapter symbolised by a hexagram formed of six lines each of which is either – – (yin) or – (yang) giving 26 = 64 alternatives. These can be arranged in a number of ways. (Knuth 2005)
The first arrangement is the King Wen Arrangement (c 1100 B.C.). King Wen is apparently a fairly loose period just meaning a very long time ago.
4 symmetric half hexagram symbols are recognised: Heaven, Earth, Fire and Water.
In this arrangement top-to-bottom mirror images (yin yang) are adjacent (odd and even numbers) and other important (same symbol and symmetrical) combinations are in prominent positions (boxed below), otherwise mathematically unsophisticated.
In the Shao Yung Arrangement (A.D. 1060)
4 extra asymmetric half hexagrams are recognised: Mountain, Wind, Thunder and Lake.
Each of 8 half hexagram symbols index both columns (above) and rows (below). Giving 8×8 = 64 combinations again.
For instance Mountain (column 2) above Lake (row 7) gives chapter 2 + (7 – 1) * 8 = 50
This makes a much more practical index for a book and facilitates divination of various sorts. This calculation method was known at the time.
Inversely chapter 50 gives 50 mod 8 (columns) = column 2 (Mountain)
and chapter 50 integer divide 8 (columns) + 1 = row 7 (Lake).
This method, which is less useful, was not known at the time.
So one might pick 2 sets of 3 long or short sticks and get the following result. 1 long and 2 short (Mountain) followed by 1 short and 2 long (Lake) and then go straight to chapter 50 for a reading.
Chapter 50 Extract
Sanskrit Poetics (c 2nd Century BCE)
A mnemonic for remembering all sequences developed in the Middle Ages:
Pingala‘s Chandahsutra (c. 200 BCE)
Syllables are short or long in length
1 long = 2 short
Pingala classified all the 16 different meters of four syllables like this:
1 meter of four short syllables SSSS
4 meters of three shorts SSSL, SSLS, SLSS, LSSS
6 meters of two shorts LLSS, LSSL, SSLL, SLLS, LSLS, SLSL
4 meters of one short SLLL, LSLL, LLSL, LLLS
1 meter of no shorts LLLL
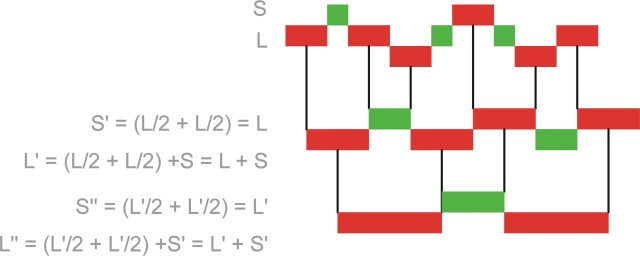
Musical Sequences and Aperiodic Tiling
Taking a Penrose P2 (Kite and Dart) aperiodic tiling marked with Ammann bars leads to a set of 5 grids at 2PI/5 rotations.
Spacing between adjacent Ammann lines, short and long intervals, is in the golden ratio. Further short cannot be followed by short and two longs cannot be followed by another long as summarised in the following decision diagram.
Composing or decomposing a musical sequence gives rise to another musical sequence and an inflated or deflated tiling.
The substitution S’=L” and L’=S+L automatically give rise to the golden ratio












Graham,
I seem to remember there was a right way an wrong way and Ken’s way, oh what fun we had scratching those dots dashes and spaces out of a solid line !
LikeLike
David,
I still do not know what the convention is for behind and beyond, do you?
Best Regards
Graham
LikeLike
Graham,
the best reference I can find is BS ISO 128-23:1995 part 23, Technical Drawing General Principles of Presentation.
A bit limited and still dosen’t really give an answer to the behind – beyond issue.
I suppose the best answer is to be consistent and clear and if in doubt use notes !
Not sure how you would draw ‘over the hills and far away ‘
Regards
David G
LikeLike
Great blog Graham and a very nice post.
I wonder if you could add some hyperlinks to some of the terms you
use in your blog. Sometimes for me it’s quite a lot to take in and I feel that
I get lost in the terminology.
For example in the article about the musical sequences you mention ” Ammann bars” or “giving rise to the golden ratio”.
Although you’ve made the subject very clear by words and drawings for me it would be nice if references could be a third. Perhaps using more references in your articles the content could would be even more insightful to a larger amount of readers.
Thanks you for sharing your thoughts and work!
All the best from Amsterdam,
Ryan
LikeLike
Hi Ryan
Thanks for your insightful remarks, they are really helpful.
Except for the stuff about Morse Code which is sort of original most of the rest comes from the later Fasicles of Knuth’s “The Art of Computer Programming” and Grunbaun and Sheppard’s “Tiling and Patterns”, though I have recoloured some of their diagrams and added some explanatory ones.
But here are some specific responses that you might find useful
I tend to use my blog as a sort of notebook and there is another post “Aperiodic Tiles” that explains Ammann bars (see Aperiodic Tiling category), https://grahamshawcross.com/2012/10/12/aperiodic-tiling/
The golden ratio comes about directly from the substitution
L / S = (L + S) / L ≡ φ = 1.61803…. There is what I think is an interesting projective derivation in another post on “Quasicrystals and Aperiodic Tiling”
Best regards from Edinburgh
Graham
LikeLike